specular holography: how

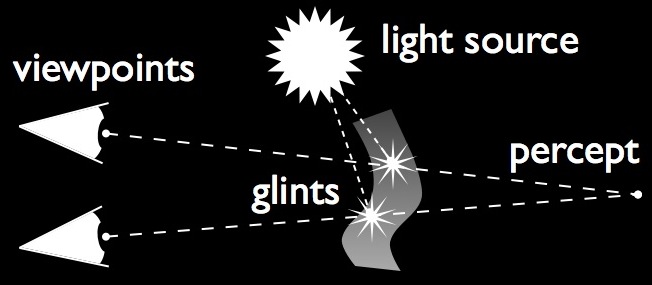
How does this work? Much like sunlight glinting on curved chrome. Every viewpoint sees a glint in different place. The trick is to control the curvature of the reflecting surface so that all sightlines through glints meet at a point somewhere off the surface in 3D space:

Since your eyes always see a glint when looking at that point, your brain decides that the light is coming from the 3D point itself.

To make the 3D illusion work for many viewpoints without distortion, each mirror has to have a unique doubly-curved shape. Here are some typical mirrors shapes that I use. Each provides a single-point depth illusion to a 90° range of viewpoints. These animations show how the glint moves as your viewpoint swings left and right:

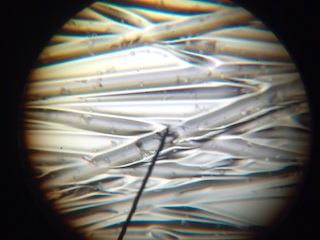
A typical specular hologram has 10,000-1,000,000 of these optics, all multiplexed into a host 2D surface. These microscope images show some example channel refractors and ridged reflectors. Each optic is uniquely shaped to keep a perceived 3D point steady (or moving predictably) as the viewpoint or light or hologram moves. The shape depends on the point, its motion, and the curvature of the host surface. Shaping and multiplexing the optical surfaces is essentially a big math problem that mixes differential geometry and combinatorial optimization. Optimization also plays a role in the artistic side of the endeavor, where I “sculpt” the scene and “draw” the outlines, shadings, and textures of its surfaces. You can see several different shading techniques in most shows. See where .